【落体の運動】斜方投射について解説
今回の記事では、斜方投射について解説します。
以前、水平投射について解説しました。
水平投射についてはコチラ↓
斜方投射は水平投射をさらにバージョンアップさせたようなものです。
斜方投射とは
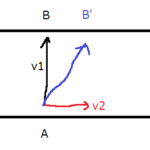
ある一定の速度で走っている車から、小球を打ち上げるとします。すると、この小球はどのような動きを見せるでしょうか。
小球の動きは…

こんな感じになります(図が雑ですみません…)
水平投射のときは、鉛直方向には自由落下、水平方向には等速直線運動と同様の運動をしていましたね。
今回の斜方投射ではどうでしょうか。
斜方投射では、
鉛直方向には、鉛直投げ上げと同様の運動をし、
水平方向には、等速直線運動と同様の運動を
しています。
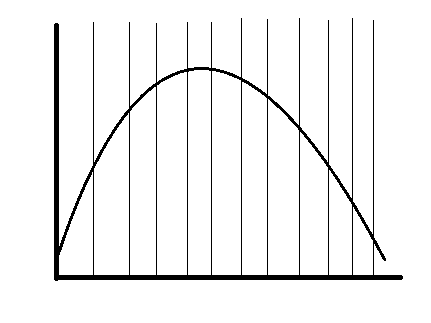
また、このときの運動の軌道は、最高点を頂点とし、鉛直線を軸とする、上に凸の放物線となっています。
って言われても、よく分からないですよね(笑)
噛み砕いて説明すると、
「この時の球体の軌道は、最高点が頂点であり、最高点を境に左右対称になっている」みたいな感じです。
等加速度運動
水平投射や斜方投射は、鉛直方向の加速度が下向きで一定の大きさです。このように加速度が一定の運動を、等加速度運動といいます。
以前、等加速度直線運動について扱ったことがありますが、水平投射や斜方投射は運動の軌道が直線ではないため、少し異なります。
等加速度直線運動についてはコチラ↓
斜方投射の公式
では、公式を導出していきます。
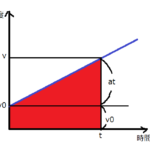
小球を水平方向と角\(\theta\)をなす向きに、大きさ\(v_0\)[m/s]の初速度で投げるとします。
以下の説明は、下図を見ながら読んでいただければと思います。
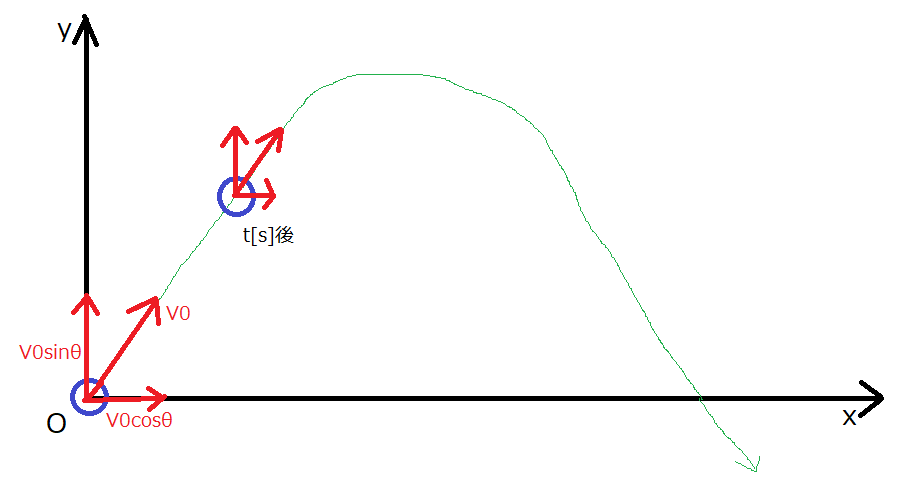
投げた点を原点とし、水平方向右向きに\(x\)軸、鉛直方向上向きに\(y\)軸を取ります。
まず、スタート地点(投げ始める瞬間)について考えます。
初速度の\(x\)成分、\(y\)成分は、それぞれ\(v_0 \cos \theta\)、\(v_0 \sin \theta\)[m/s]になりますね。
では、続いて\(t\)[s]後について考えます。
\(x\)軸方向、つまり、鉛直方向には等速直線運動と同様の運動をします。
(等速直線運動についてはコチラ↓を参考にしてください。)
したがって、\(t\)[s]後の速度の\(x\)成分(\(v_x\))は、
\[v_x = v_0 \cos \theta \text{ ・・・(31)}\]
となります。続いて、変位\(x\)は、
\[x=v_0 \cos \theta \cdot t\text{ ・・・(32)}\]
です。
今度は\(y\)軸方向について考えていきます。
\(y\)軸方向(鉛直方向)には、鉛直投げ上げと同様の運動をするんでしたね。
(鉛直投げ上げについてはコチラ↓を参考にしてください。)
したがって、\(t\)[s]後の速度の\(y\)成分\(v_y\)は、
\[v_y = v_0 \sin \theta -gt \text{ ・・・(33)}\]
\(t\)[s]後の座標\(y\)は、
\[y=v_0 \sin \theta \cdot t – \frac{1}{2}gt^2 \text{ ・・・(34)}\]
となります。
では、斜方投射の公式を整理します。
\[v_x=v_0 \cos \theta\]
\[x=v_0 \cos \theta \cdot t\]
\[v_y = v_0 \sin \theta -gt\]
\[y=v_0 \sin \theta \cdot t – \frac{1}{2}gt^2\]
例題
地上の点から小球を、速さ\(49.0\)m/sで図のような向きで斜方投射させた。\(\sin \theta=\frac{4}{5}\)、\(\cos \theta = \frac{3}{5}\)とし、重力加速度の大きさを\(9.80\)m/s2とする。
(1)初速度の水平成分と鉛直成分の大きさ\(v_{0x}\)、\(v_{0y}\)[m/s]を求めよ。
(2)最高点に達するまでの時間\(t_1\)[s]と、その高さ\(h\)[m]を求めよ。
(3)落下点に達するまでの時間\(t_2\)[s]と水平到達距離\(l\)[m]を求めよ。
(1)\(v_{0x}=v_0 \cos \theta = 49.0 \cdot \frac{3}{5} = 29.4\)
よって、\(v_{0x} = 29.4\)m/s
\(v_{0y}=v_0 \sin \theta = 49.0 \cdot \frac{4}{5} = 39.2\)
よって、\(v_{0y} = 39.2\)m/s
(2)最高点では速度の\(y\)成分が0になっていますから、
\(v_y = v_0 \sin \theta – gt\)より、
\(0 = 39.2-9.80 \cdot t_1\)を解くと、
\(t_1 = 4.00\)s
\(y=v_0 \sin \theta \cdot t -\frac{1}{2}gt^2\)より、
\(h=39.2 \cdot 4.00 – \frac{1}{2} \cdot 9.80 \cdot 4.0^2\)
これを解くと、\(h=78.4\)m
(3)落下点では高さが0mですから、\(y=v_0 \sin \theta \cdot t -\frac{1}{2}gt^2\)より、
\(0=39.2 \cdot t_2 – \frac{1}{2} \cdot 9.80 \cdot {t_2}^2\)
これを解くと、\(t_2=8.00\)s
\(x=v_0 \cos \theta \cdot t\)より、\(l=29.4 \cdot 8.00 = 235.2\)
したがって、\(l=235.2\)m
地上の点から小球を、水平方向と角\(\theta\)をなす向きに大きさ\(2v_0\)[m/s]の初速度で投げる。重力加速度の大きさを\(g\)[m/s2]とする。必要であれば、\(2 \sin \theta \cos \theta = \sin 2\theta\)を用いよ。
(1)最高点に達するまでの時間\(t_1\)[s]とその高さ\(h\)[m]を求めよ。
(2)落下点に達するまでの時間\(t_2\)[s]と水平到達距離\(l\)[m]を求めよ。
(3)初速度の大きさを変えずに、角\(\theta\)を変えて投げるとき、小球を最も遠くまで投げるための角\(\theta_0\)を求めよ。
(1)最高点では\(v_y\)が0になりますので、
\(0 = 2v_0 \sin \theta -gt_1\)
よって、
\[t_1 = \frac{2v_0 \sin \theta}{g} \text[s]\]
\(y = v_0 \sin \theta \cdot t -\frac{1}{2}gt^2\)より、
\(h = 2v_0 \sin \theta \cdot \frac{2v_0 \sin \theta}{g} -\frac{1}{2}g \cdot \left(\frac{2v_0 \sin \theta}{g} \right)^2\)
これを整理すると…
\[h = \frac{2v_0^2 \sin^2 \theta}{g}[m]\]
(2)落下点では鉛直方向の変位が0になりますから、\(y = v_0 \sin \theta \cdot t -\frac{1}{2}gt^2\)より、
\(0 = 2v_0 \sin \theta \cdot t_2 – \frac{1}{2}g{t_2}^2\)
これを整理すると、
\[t_2 = \frac{4v_0 \sin \theta}{g}[s]\]
\(x = v_0 \cos \theta \cdot t\)より、
\(l = 2v_0 \cos \theta \cdot \frac{4v_0 \sin \theta}{g}=\frac{8v_0^2 \sin \theta \cos \theta}{g}\)
\(2\sin \theta \cos \theta = \sin 2 \theta\)より、
\[l = \frac{4v_0^2 \sin 2 \theta}{g}[m]\]
(3)最も遠くに飛ぶときは、\(l\)の値が最大になります。
初速度の大きさは変えないので、\(v_0\)は固定です。\(g\)も定数ですから、変わりません。
したがって、\(\sin 2 \theta\)が最も大きくなる時に最も遠くに飛びます。
\(0^\circ \text{≦} \theta \text{≦} 90^\circ\)の範囲で考えた時、\(\theta = 90^\circ\)のときに最大値\(1\)をとります。
ですから、\(2 \theta_0 = 90^\circ\)より、
\[\theta_0 = 45^\circ\]
例題②の最後の問題は、三角関数の2倍角の定理を理解しておく必要がありますね…
まとめ
今回は斜方投射について取り上げました。
- 斜方投射は、鉛直方向には鉛直投げ上げと同様の運動をしている。
- 水平方向には等速直線運動と同様の運動をしている。
- 物体の運動の軌道は、最高点を頂点とする上に凸の放物線となる。
- 加速度が一定の運動を、等加速度運動という。
というわけで、今回の記事は以上です。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。