【力学】加速度②(等加速度直線運動)
この記事では、等加速度直線運動について解説していきます。加速度の考え方については、↓の記事で解説しています。
Contents
等加速度直線運動とは
等加速度直線運動とは、その名の通り、加速度が一定の直線運動です。
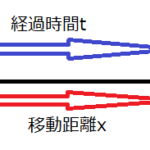
等速直線運動というのは、速度が一定の運動でしたが、等加速度直線運動では速度の変化が一定です。
等速直線運動についてはコチラ↓
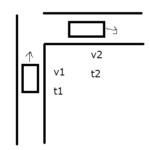
停止している自動車があったとしましょう。この車が3秒後に6m/sになったとします。さらに3秒後(つまり6秒後)に12m/sになったとします。この場合、最初の3秒とその後の3秒では、速度の変化量は同じであると言えます。
このように、一直線上を一定の加速度で進む運動を等加速度直線運動といいます。
速度
等加速度直線運動には3つの公式があります。その3つの公式を導出していきましょう。
ここでは、一定の加速度\(a[m/s^2]\)で速度が変化する時の等加速度直線運動を考えます。
時刻0での速度を\(v_0\)とします。この速度を初速度といいます。
速度は時間\(t[s]\)後には\(at\)だけ増加します。
よって、時刻\(t[s]\)における速度\(v[m/s]\)は次のようになります。
\[v=v_0+at\text{・・・(13)}\]
(13)式は、グラフで描くと下図のようになります。

\(v-t\)グラフですね。直線の傾きは加速度\(a\)、\(v\)軸の切片は初速度\(v_0\)です。
一次関数のグラフですね。
変位
今度は変位について考えてみましょう。
先程のグラフの中で、変位はどこに表れているかといいますと、グラフの面積です。
なぜ面積が変位になるかというと…この辺をちゃんと理解するためには数学の微分積分の知識が必要になってきますので、ここでは割愛しておきます。
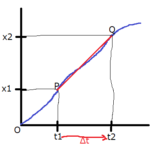
では、面積を求めてみましょう。求める面積の部分を分かりやすく加工したのが、下図です。
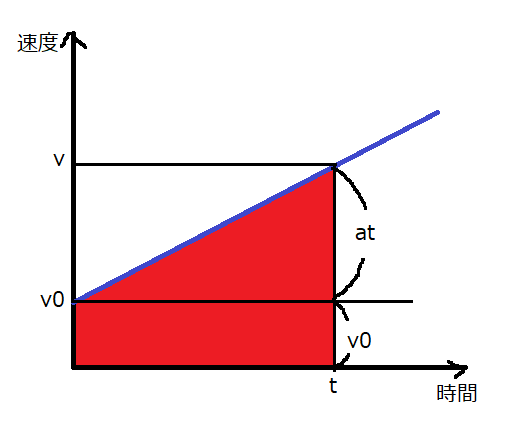
赤で塗りつぶした部分の面積を求めます。台形の面積の求め方は、(上底+下底)×高さ÷2でしたね。
上底は\(v_0\)です。下底は\(v_0+at\)です。高さは\(t\)です。これらを台形の面積の公式に代入すると、
\((v_0+v_0+at)\times t \div 2 = (2v_0t+at^2) \div 2 = v_0t+\frac{1}{2}at^2\)
したがって、時刻\(t[s]\)での変位\(x[m]\)は、
\[x=v_0t+\frac{1}{2}at^2\text{・・・(14)}\]
また、(13)式と(14)式から、\(t\)を消去します。
(13)式を変形して、\(t=\frac{v-v_0}{a}\) これを(14)式に代入します。すると…
\(x=v_0\cdot\frac{v-v_0}{a}+\frac{1}{2}a\left(\frac{v-v_0}{a}\right)^2\)
これを整理すると、
\[v^2-v_0^2=2ax\text{・・・(15)}\]
例題
\(1.0m/s\)の速さで動いていた物体が、一定の加速度\(1.5m/s^2\)で加速した。
(1)2.0秒後の物体の速さは何\(m/s\)か。
(2)2.0秒後までに物体は何\(m\)進むか。
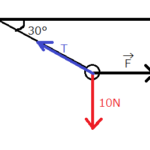
(3)この後、ブレーキをかけて一定の加速度で減速して、\(20m\)進んだ地点で停止した。このときの加速度の向きと大きさを求めよ。
(1)\(v=v_0+at\)より、
\(v=1.0+1.5\times 2.0=4.0\)
したがって、\(4.0m/s\)
(2)\(v^2-v_0^2=2ax\)より、
\(4^2-1^2=2\cdot 1.5\cdot x\)
\(x=5.0\)
したがって、\(5.0m\)
(3)\(v^2-v_0^2=2ax\)より、
\(0^2-4^2=2a\cdot20\)
よって、\(a=-0.4\)
したがって、運動の向きと逆向きに\(-0.4m/s^2\)
初速度\(v_0\)と速度\(v\)の値がどの値になるのかを整理してから式を立てましょう。(3)の場合、初速度は\(1.0m/s\)ではなく\(4.0m/s\)になるので注意が必要です。
まとめ
初速度\(v_0\)、加速度\(a\)、時刻\(t\)、変位\(x\)とすると、等加速度直線運動において以下の3つの式が成り立ちます。
- \(v=v_0+at\)
- \(x=v_ot+\frac{1}{2}at^2\)
- \(v^2-v_0^2=2ax\)
というわけで、この記事の内容はここまでです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。