【2次関数】センター試験を解いてみる(2017年度)
今回は、2017年度のセンター試験(数学ⅠA)の2次試験の問題を解いていきたいと思います。
センター試験公式サイトは2017年以前の問題については紹介がないので、別のページから拾ってきてます。
問題

解説
セソタチツテト
頂点を求める問題は平方完成をするだけで答えが導き出せます。平方完成についてはコチラ
\(g(x)=x^2-2(3a^2+5a)x+18a^4+30a^3+49a^2+16\)を平方完成すると…
\(g(x)=\{x-(3a^2+5a)\}^2+9a^4+24a^2+16\)となります。
したがって頂点は、点(\(3a^2+5a,9a^4+24a^2+16\))ですね。
ナニヌネ
頂点の\(x\)座標の最小値を求める問題です。頂点の\(x\)座標は、\(3a^2+5a\)でしたね。\(a\)についての2次関数の式とみなすことができますね。
\(3a^2+5a\)を\(h(a)\)としましょうか。この\(h(a)\)の最小値が\(g(x)\)の頂点の\(x\)座標の最小値になると考えることができます。
\(h(a)=3a^2+5a\)を平方完成してみましょう。すると…
\[h(a)=3(a+\frac{5}{6})^2-\frac{25}{12}\]
となります。下に凸のグラフでは頂点が最小値を取ります。したがって、\(g(x)\)の頂点の\(x\)座標の最小値は、\(-\frac{25}{12}\)となります。
ノハ
今度は頂点の\(y\)座標の最小値ですね。
\(a^2=t\)とすると、頂点の\(y\)座標は、\(9t^2+24t+16\)となります。では、\(9t^2+24t+16\)を\(k(t)\)として、平方完成してみましょう。すると…
\[k(t)=9(t+\frac{4}{3})^2\]
となります。したがって、\(h(t)\)の頂点は点(\(-\frac{4}{3},0\))ですね。グラフを描くと以下のようになるでしょう。
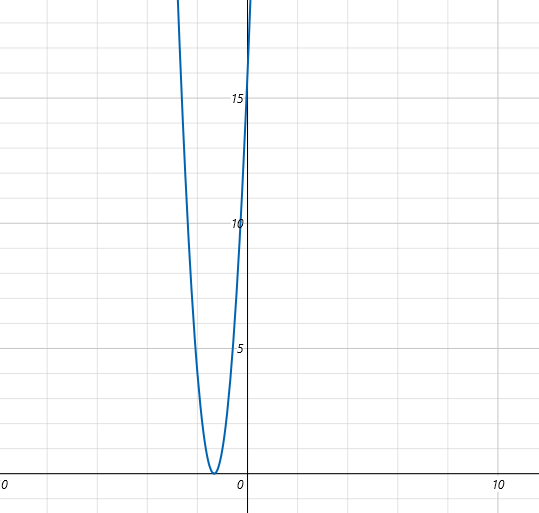
ただし、\[\(a\)は実数ですから、\(a^2=t\)より\(t\)は必ず正の値もしくは0になりますね。負の値になることはあり得ません。なので、グラフの\(t\text{≧}0\)の部分のみを考えなければなりません(このグラフは横軸が\(t\)です)。
グラフを見れば、\(k\)軸(縦軸)より左側を除外すれば、\(t=0\)の時に最小値を取ることが分かりますね。関数式に\(t=0\)を入れると…最小値は16であることが分かります。
したがって、\(t=0\)つまり\(a=0\)のときに頂点\(y\)は最小値16を取ります。
まとめ
今回の問題を解く上での重要ポイントは…
- \(x\)でなく\(a^2\)などでも2次関数とみなして問題を解き進めることがある。
- 実数は2乗すると必ず正の値・もしくは0になる。
という部分ですね。
というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。
