【2次関数】センター試験の問題を解いてみた(2018年度②)
今回は、2018年度のセンター試験の追試問題を解いていきたいと思います。
問題【前編】
解説【前編】
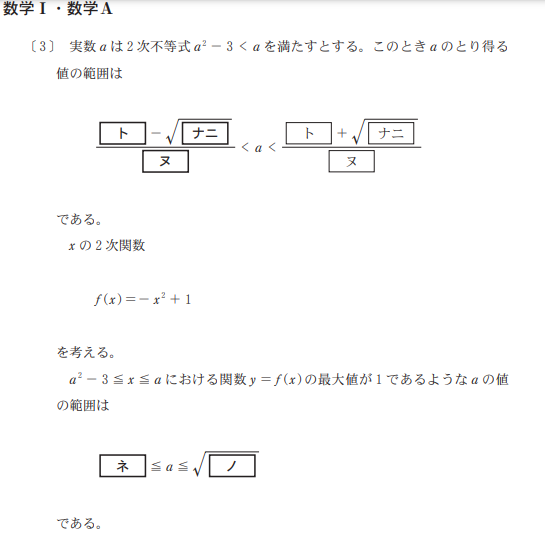
ト・ナ・ニ・ヌ
\(a^2-3<a\)を解けばいいので…
\[\frac{1-\sqrt{13}}{2}<a<\frac{1+\sqrt{13}}{2}\]
が答えです。
ネ・ノ
最大値が1であるような\(a\)の範囲ですね。
このグラフ、\(y=-x^2+1\)という式ですが、頂点は点(0,1)であり、上に凸のグラフなので頂点が最大値になることが読み取れます。したがって、最大値が1であるということは、この頂点が定義域の中にある状態のときの\(a\)の範囲を求めればいいわけです。
ここで定義域は\(a^2-3\text{≦}x\text{≦}a\)ですから、\(a^2-3\text{≦}0\)と\(0\text{≦}a\)を共に満たす\(a\)の範囲が答えです。
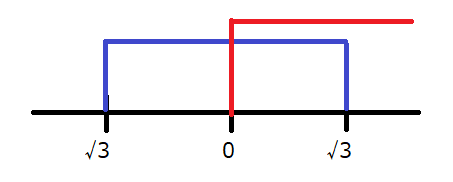
したがって、答えは\(0\text{≦}a\text{≦}\sqrt{3}\)です。
問題【後編】
解説【後編】
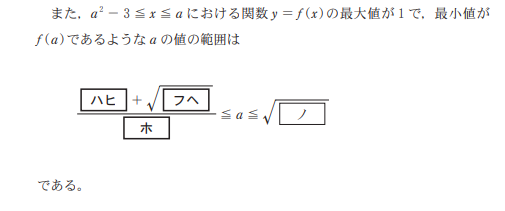
\(f(a)\)が最小値を釣るような\(a\)の値の範囲を求める問題です。
\(f(a)\)が最小値を取るということは、定義域の右端で最小値を取るということです。グラフを描いてみると、このような感じになるかと思います。
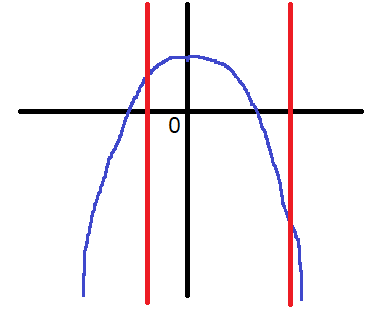
最大値が1という風に指定がありますね。これは、頂点が最大値になるということであり、定義域の範囲の中に頂点が含まれているということです。先程のネとノで求めた答えを使えますね。ただし、そのままでは\(f(a)\)が最大値を取ってしまう(定義域の右端が頂点と重なる)場合も含んでしまいます。その可能性を除外する必要があるので、\(0<a\text{≦}\sqrt{3}\)になりますね。これを(1)条件とします。
さらに、もう1つの条件を加える必要があります。それは、頂点の\(x\)座標から\(f(a)\)の\(x\)座標までの距離(この距離をA距離とする)が、頂点の\(x\)座標から\(f(a^2-3)\)の\(x\)座標までの距離(この距離をB距離とする)より長くならなければならない、というものです。つまり、\(f(a)\)より\(f(a^2-3)\)の方が頂点に近くなるわけですね。
A距離は\(a\)となります。B距離は\(3-a^2\)となります(負の方向への距離なので注意・0から-5までの距離が-5ではなく5になることと原理は同じ)。
\(a\text{≧}3-a^2\)が成立すれば、\(f(a)\)で最小値を取ると判断することができます。これを解くと、
\[\frac{-1-\sqrt{13}}{2}\text{≧}a\]
または
\[a\text{≧}\frac{-1+\sqrt{13}}{2}\]
となります。これを(2)条件とします。ちなみに、\(\sqrt{13}\)は3~4とみなすことができます。
(1)と(2)を同時に満たす\(a\)の値の範囲は…
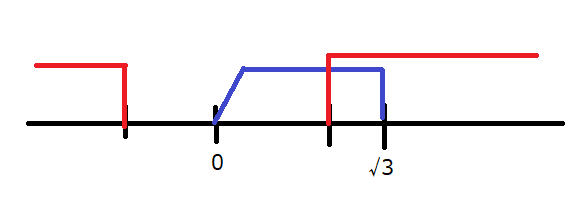
したがって、条件を満たす\(a\)の範囲は…
\[\frac{-1+\sqrt{13}}{2}\text{≦}a\text{≦}\sqrt{3}\]
となります。
まとめ
今回の問題を解く上での重要ポイントは…
- 上に凸のグラフでは定義域の中に頂点が含まれていれば、頂点が最大値になる。
- 上に凸のグラフにおいて、定義域の右端で最小値を取るためには、頂点から定義域の左端と右端までの距離を考える必要がある。
こんな感じでしょうか。後半の問題はカギを閃くことができるかどうかにかかっていると思います。
というわけで、今回はここで終わりです。何か参考になる情報があれば嬉しいです。
最後までお読みいただき、ありがとうございました。
